What happens when you focus lenses from infinity to shorter distances?
What’s the relationship between the main features of a lens?
05/18/2017Traffic lens helps artificial intelligence
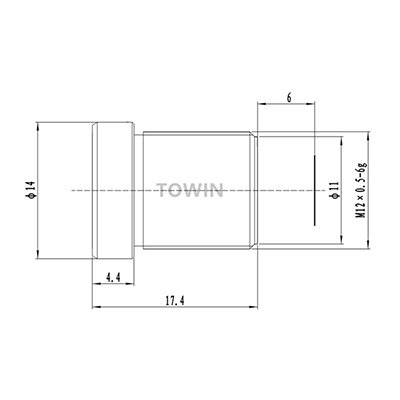
02/04/2020To focus on shorter distances, s-mount lenses have to be “unscrewed” . On first glance this seems to be very different from larger Lenses like C- or CS-mount Lenses, that provide a focus ring. If the focusing ring is turned however also in larger lenses the position of a lens package from the sensor is increased. (There are a few exception of lenses that offer more than one lens package that are moved synchrously, one of this maybe towards the sensor) .
Well over 95% of all lenses work as described here:
May the lens be focussed on infinity. What happens when you increase the distance of the lens package from the sensor, for example by unscrewing or by turning the focus ring?
- The _maximum_ object side viewing angle of the lens stays the same… because the optics does not change
- The _maximum_ image side viewing angle of the lens stays the same… because the optics does not change
- The _maximum_ amount of pixels the lens can handle is still the same … because the optics does not change
- The F# changes to the “Working F#” (also called effective F#) :
The F# of a lens is only defined for infinite distance. When focused to infinity the focal point of the lens is right on the sensor.The F# is then defined as : Focal length, divided by the Entry-Pupil-Diameter (= the appearant diameter of the “hole” in the lens when you look from object side = “EPD”)The working F# (‘wF#) is defined a little different : wF# = (focal length + amount unscrewed) /EPD = F# + (amount unscrewed / EPD)
![\[wF\# = (1 + M) * F\#\]](https://www.optowiki.info/wp-content/ql-cache/quicklatex.com-9f02739cbee64d6d5c9164ace5864659_l3.svg "Rendered by QuickLaTeX.com")
Example 1:
For a 1:1 magnification (object size = sensor size), you have to unscrew by the focal length. 12mm for a 12mm lens : 4mm for a f=4mm lens , 50mm for a 50mm lens)
For the 1:1 case we get
![\[wF\# = 2* F\#\]](https://www.optowiki.info/wp-content/ql-cache/quicklatex.com-ec7ee20fcf9be156726c1aa61b47f093_l3.svg "Rendered by QuickLaTeX.com")
(because the amount unscrewed = f , so we get
![\[wF\# = 2 * (focal length / EPD ) = 2*F\# \]](https://www.optowiki.info/wp-content/ql-cache/quicklatex.com-7e9d6476ca6d0ce3a1ecf0f5ad27fbc7_l3.svg "Rendered by QuickLaTeX.com")
)
We get the same result from the above formula with M=1 :
![\[wF\# = 2 F\#\]](https://www.optowiki.info/wp-content/ql-cache/quicklatex.com-ac8d8f17dc09aba9d5d6e69470c9976d_l3.svg "Rendered by QuickLaTeX.com")
Example 2:
For the object at infinity, no unscrewing is needed, so we have wF# = F#.
The magnification for objects at infinity is zero, because the sensor is small and at infinite distances the lens sees infinite much. (Hundreds of galaxies at the night sky, for example). So we get from the formula above :
![\[wF\# = (1 + M) F\# = (1 + 0)F\# = F\#\]](https://www.optowiki.info/wp-content/ql-cache/quicklatex.com-a75a60e150f5a7471bc9018b2e5a30c7_l3.svg "Rendered by QuickLaTeX.com")
- The brightness of the image changes:
The amount of light that reaches the sensor is determined by wF#, the working F#. wF# depends on the diameter of the Entry pupil, but the brightness depends on the area of the entry pupil.
wF#, the working F# of a 1:1 lens is
wF# = 2 F# = twice the wF# at infinity \]
So the brightness decreases by factor 2^2 = 4 compared to the brightness at infinity
- In general the resolution decreases: The smallest possible point diameter that a diffraction limited (read”perfect”) lens can generate is given by the Rayleigh diameter :
![\[ D = 2 * 1.22 * wF\# * Wavelength \]](https://www.optowiki.info/wp-content/ql-cache/quicklatex.com-191bfb4ff2dbfda750dc25e4c9a99eb1_l3.svg "Rendered by QuickLaTeX.com")
The resolution is half that diameter R = D/2.
- The Field of view gets smaller: Because the lens is not telecentric (but “entocentric”), the light arrives at some Angle > 0 in the corners of the sensor. We can imagine this as an image side (half) viewing angle. That angle is called (max) Chief ray angle) When the lens is in infinity position. When we increase the distance to the sensor, tha maximum angle stays the same, but some of the light will no longer reach the sensor. This means, only a smaller fan angle on image side can be used. This implicated that also only a smaller angle on object side can be used!
- The magnification changes. This is because the sensor keeps its size and the visible Object size gets smaller, see above
- The distortion in general gets better : Distortion of each lens is larger in the corners of the field of view than in the center. Because we use a smaller object and image side angle now, we also don’t use the old colrners of the image any more. Therefore we don’t use the rim of the lens elements
- There working distance changes, because the ratio of object distance and image distance is the Magnification, which changed.
- The Chief Ray Angle CRA changes. This it the off axix angle at which the light arrives in the sensor corners.
By changing the working distance from infinity to a shorter distance, maybe even below the MOD, these angles change. But for these new angles the lens was never designed, so the performance MUST suffer.
Whether the performance is still good enough depend on you application and especially on the sensor pixel size
For an 1:1 lens for example is the imageF# = object side F#, the resolution on image and object side is the same (and not factor 2 lower than with entocentric lenses. Also the image brightness does not decrease by factor 4.